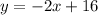Question

Write an equation if a line perpendicular to the given equation through the given point

Answer 1

The given equation is

`y=(1)/(2)x-6`

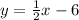
The slope of the given equation is 1/2 (the coefficient of x).

Then, we use the perpendicularity definition to find the slope of the new line

`\begin{gathered} m\cdot m_1=-1 \\ m\cdot(1)/(2)=-1 \\ m=-2 \end{gathered}`

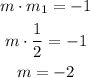
Then, we use the point (6,4), the slope -2, and the point-slope formula to find the equation

`\begin{gathered} y-y_1=m(x-x_1) \\ y-4=-2(x-6) \\ y-4=-2x+12 \\ y=-2x+12+4 \\ y=-2x+16 \end{gathered}`

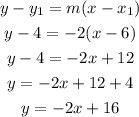
Hence, the equation of the new perpendicular line is

`y=-2x+16`