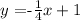Solution:
Let us denote by L1 the line represented by the following equation:
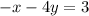
If we convert this equation to slope-intercept form, we get:
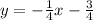
then, the slope of L1 would be -1/4. Now, the slopes of parallel lines are equal. According to this, we have that the provisional equation of the line parallel to L1 is:
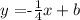
Now, since this line contains the point (0,1), this means that the y-intercept b is equal to 1. So, the equation of the line parallel to L1 is:
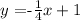
then, we can conclude that the correct answer is: