Given data:
* The angle of the inclined plane is

* The mass of the object is m = 250 g.
Solution:
The diagrammatic representation of the given case is,
The force acting down the inclined plane due to the weight of an object is,
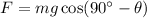
where g is the acceleration due to gravity,
Substituting the known values,
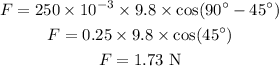
The normal force acting on the object is,
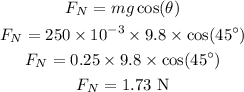
The frictional force in terms of the normal force is,
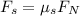
where,
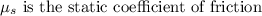
As the object is in a static state under the action of force, thus, the frictional force is balancing the force acting on the object down the inclined plane (F_s = F)
Substituting the known values,
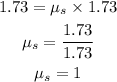
Hence, the coefficient of friction of an object on an inclined plane is 1.