Question

Two 2 cm-diameter disks spaced 1.926 mm apart form a parallel-plate capacitor. The electric field between the disks is 576,184.575 V/m. An electron is launched from the negative plate. It strikes the positive plate at a speed of 31,724,040.891 m/s. What was the electron's speed as it left the negative plate?

Answer 1

If we know the electric field and the charge of a particle, we can find out the force it feels. This can be written as:

`\vec{F}\text{ = }q\vec{E}=1.6*10^(-19)*576185.575=9.2189692*10^(-14)N`

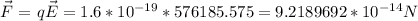
Then, knowing the force, we can find out its acceleration by Newton's second law, thus:

`a=(F)/(m)=(9.2189692*10^(-14))/(9.1093837*10^(-31))=1.012029958*10^(17)(m)/(s)`

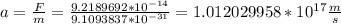
We can then rearrange Torricelli's formula in order to obtain the initial velocity:

`v_0=\sqrt[\placeholder{⬚}]{(v_f)^2-2a\Delta s}`

Then, replacing our values we get:

`v_0=\sqrt[\placeholder{⬚}]{(31724040.891)^2-2*1.012*10^(17)}=24831045.7(m)/(s)`

Then, our final answer is v0=24831045.7 m/s