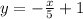Question

A line passes through the points (-5, 2) and (10, -1). Which is the equation of the line? 1 OyX+1 yX+3 y-5x-23 Oy=5X+27

Answer 1

The line passes through the points (-5, 2) and (10,-1) and we need to find the equation of the line.

Step 1: We will label this coordinates as follows:

`\begin{gathered} x_1=-5 \\ y_1=2 \\ x_2=10_{} \\ y_2=-1 \end{gathered}`

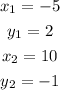
Step 2. We calculate the slope "m" with the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

substituting our values:

`m=(-1-2)/(10-(-5))`

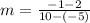
solving the operations we find that the slope is:

`\begin{gathered} m=(-3)/(10+5) \\ m=-(3)/(15) \\ m=-(1)/(5) \end{gathered}`

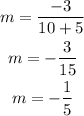
(Note: in the last line we simplified the fraction 3/15 to 1/5 dividing by 3)

Step 3. We use the the point-slope squation which is:

`y=m(x-x_1)+y_1`

And we substitute all of the known values of the slope m, and the point (x1, y1) which is (-5,2):

`y=-(1)/(5)(x-(-5))+2`

Simplifying the expression:

`y=-(1)/(5)(x+5)+2`
`\begin{gathered} y=-(1)/(5)x-(1)/(5)(5)+2 \\ y=-(x)/(5)-1+2 \end{gathered}`

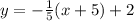
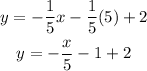
we add the -1 +2 and get the final result:

`y=-(x)/(5)+1`

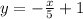
Answer:

`y=-(x)/(5)+1`