Start by putting the possible integers your friend can select
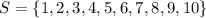
Then, call the 2 possible events as A and B, and what are the possible integers in each event:
A= Be more than 6
B= The number is odd
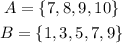
The probability of the union of two events can be calculated as:
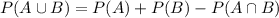
Then,

Finally,
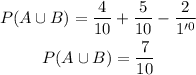
Answer:
the probability that the number will be more than 6 or odd is: 7/10