Question

A furniture shop refinishes cabinets. Employees use two methods to refinish cabinets. The method I takes 0.5 hours and the material costs $10. Method II takes 1.5 hours, and the material costs $6. Next week, they plan to spend 185 hours in labor and $1540 in material for refinishing cabinets. How many cabinets should they plan to refinish with each method?

Answer 1

Method I: Let A be the number of cabinets refinish with method I

Method II: Let B be the number of cabinets refinish with method II

Time:

Method I: 0.5A

Method II: 1.5B

Cost:

Method I: 10A

Method II: 6B

Next week, they plan to spend 185 hours in labor and $1540 in material for refinishing cabinets:

`\begin{gathered} 0.5A+1.5B=185 \\ 10A+6B=1540 \end{gathered}`

Solve the system of equations above to find the number of cabinets refinish with each method:

1. Solve A in the second equation:

`\begin{gathered} 10A+6B=1540 \\ 10A=1540-6B \\ A=(1540)/(10)-(6)/(10)B \\ \\ A=154-0.6B \end{gathered}`

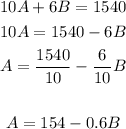
2. Substitute the A in the first equation by the value you get above:

`\begin{gathered} 0.5(154-0.6B)+1.5B=185 \\ 77-0.3B+1.5B=185 \\ 77+1.2B=185 \\ 1.2B=185-77 \\ 1.2B=108 \\ B=(108)/(1.2) \\ \\ B=90 \end{gathered}`

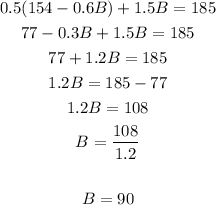
3. Use the value of B to solve A:

`\begin{gathered} A=154-0.6B \\ A=154-0.6(90) \\ A=154-54 \\ A=100 \end{gathered}`

Solution:

A=100

B=90

Then, with Method I should be refinish 100 cabinets, and with method II should refinish 90 cabinets