ANSWER
The maximum amount of water produced is 45.09 g H20
Step-by-step explanation
Given data
The mass of ammonia = 66.8g
The mass of oxygen = 66.8 g
To find the maximum amount of water produced in grams, follow the steps below
Step 1: Write the balanced equation of the reaction
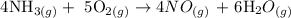
From the above reaction, you will see that 4 moles of ammonia and 5 moles of oxygen produce 4 moles of nitrogen oxide and 6 moles of water
Step 2: Find the number of moles in each of the reactants using the below formula
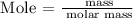
Recall, that the molar mass of ammonia is 17.031 g/mol and the molar mass of oxygen is 32 g/mol
For ammonia
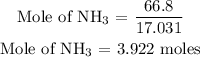
For oxygen
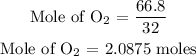
Step 3: Find the limiting reactant of the reaction.
To find the limiting reactant, divide the number of moles by the coefficient of each reactant. Hence, the reactant with the least number of moles becomes the limiting reactant.

From the above calculations, you will see that oxygen has the least number of moles per wt, hence, oxygen is the limiting reactant
Step 4: Find the number of moles of water using a stoichiometry ratio.
To find the moles of water, we use the moles of the limiting reactant
Recall, that the mole of oxygen is 2.0875 moles
From the reaction, 5 moles of oxygen give 6 moles of water
Let x represents the number of moles of water
Mathematically, we have

Hence, the number of moles in water is 2.505 moles
Step 5: Find the mass of water in grams using the below formula
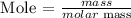
Recall, that the molar mass of water is 18.0 g/mol
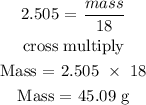
Therefore, the maximum amount of water produced is 45.09 g H20