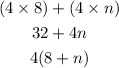
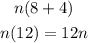
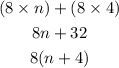
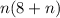
We just expanded and simplify the expressions in the questions.
We would be simplifying the options as well to get the equivalent options to the question
Box 1 gives
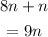
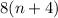
Box 2 gives 8(n+4)
Box 3 gives
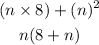
Box 3 gives n(8+n)
For Box 4
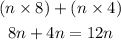
Box 4 gives 12n
Compairing the questions with the given expressions in the box, it can be seen that
Hence, n(8+4)=12n is equivalent to box 4 which is (nx8)+(nx4)=12n
Also, (8xn)+(8x4)= 8(n+4) is equivalent to box 2 which is 8(n+4)
n(8+n) is equivalent to Box 3 which is (nx8)+(n)²