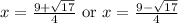Given the Quadratic Equation:
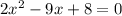
You need to use the Quadratic Formula in order to solve it:
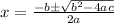
Notice that the equation is written in this form:
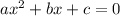
Then, in this case:
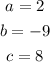
Now you can substitute values into the formula and evaluate:
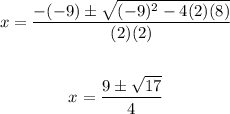
Notice that you get two values:
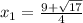
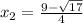
Hence, the answer is: