ANSWER
y = x² + 10x + 29
Step-by-step explanation
The standard form of a quadratic function is,
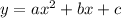
In this problem, we know what is the vertex of the graph, so we can start by writing the equation in vertex form,
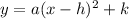
Where (h, k) is the vertex.
In this case, the vertex is at (-5, 4),
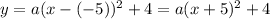
Any value of a will satisfy the condition that the vertex is at (-5, 4), so we can use a = 1 - note that we have an infinite number of quadratic functions that satisfy this condition, but we have to write one.
Now, to write it in standard form, expand the binomial squared,
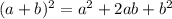
So the equation is,
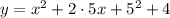
Solve the products and exponents, and add like terms,
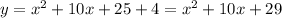
Hence, a quadratic function whose vertex is at (-5, 4) is y = x² + 10x + 29.