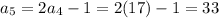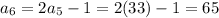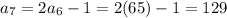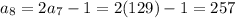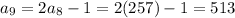Question

For the question below identify each with a coordinating response. Be sure to clearly label each part of your response as part a, part b, and part c.

Answer 1

Given the sequence:

`3,5,9,17,...`

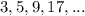
Part A:

You can identify that each term is found by multiplying the previous term by 2 and then subtracting 1 to the Product.

Then, you can write the following equation to represent the pattern:

`a_n=2a_((n-1))-1`

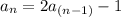
Where the previous term is:

`a_((n-1))`

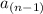
And the nth term is:

`a_n`

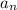
Parts B and C:

You know the first four terms.

Then, using the equation found in Part A, you can determine that the next five terms are:

`a_5=2a_4-1=2(17)-1=33`

`a_6=2a_5-1=2(33)-1=65`
`a_7=2a_6-1=2(65)-1=129`
`a_8=2a_7-1=2(129)-1=257`
`a_9=2a_8-1=2(257)-1=513`
`a_(10)=2a_9-1=2(513)-1=1025`

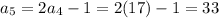
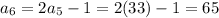
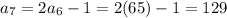
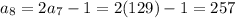
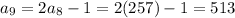
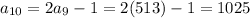
Hence, the answers are:

Part A: Each term is found by multiplying the previous term by 2 and then subtracting 1 to the Product:

`a_n=2a_((n-1))-1`

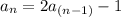
Part B:

`\begin{gathered} a_5=33 \\ a_6=65 \\ a_7=129 \\ a_8=257 \\ a_9=513 \\ a_(10)=1025 \end{gathered}`

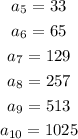
Part C:

`a_5=2a_4-1=2(17)-1=33`

`a_6=2a_5-1=2(33)-1=65`
`a_7=2a_6-1=2(65)-1=129`
`a_8=2a_7-1=2(129)-1=257`
`a_9=2a_8-1=2(257)-1=513`