a) Girls: Mean=46 Median=50 Mode=50 and 81
Boys: Mean=34 Median=33 Mode= None
Mean a good measure to give an idea of the whole but very sensitive to higher and lower figures inserted, on the table.
Median:
This is a measure more resistant to the lower and upper figures. Much more reliable.
------
1) Let's compute the Measures of the Center, namely mean, median, mode:
Let's set a table, for the Music Downloads 6th graders, organizing it from the least to the greatest:
a) Let's calculate the Mean for the Girls
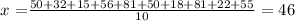
Let's Calculate the Median:
This is a measure more resistant to the lower and upper figures. So a Median is more trustable in many times.
Since there 10 observations (even number) the Median for the girls are 50+ 50/2 = 50
The Mode, the number that repeats itself more often in this case, there are two 50 and 81 downloads. A bimodal observation. 2 modes.
For the boys:
Similarly for the boy, the Mean is the sum over 10 = 34
The Median for the boys is the sum of the 5th and 6th observation, over 2:
25+41/2 66/2=33
Mode
There is no mode. No number repeats itself for the boys.