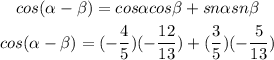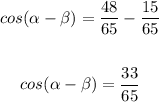Question

Find exact value of cos(alpha-beta) given sin alpha equals 3/5 and cos beta equals -12/13

Answer 1

Remember that

`cos(\alpha-\beta)=cos\alpha *cos\beta+sin\alpha *sin\beta`

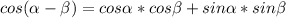
step 1

Find out the cosine of angle alpha

Remember that

`\begin{gathered} sin^2\alpha+cos^2\alpha=1 \\ sin\alpha\text{=}(3)/(5)\text{ ---> given} \end{gathered}`

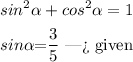
substitute

`((3)/(5))^2+cos^2\alpha=1`

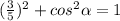
The angle alpha lies on the II quadrant -----> the value of the cosine is negative

`\begin{gathered} cos^2\alpha=1-(9)/(25) \\ cos^2\alpha=(16)/(25) \\ cos^\alpha=-(4)/(5) \end{gathered}`

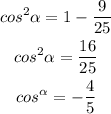
step 2

Find out the sine of the angle beta

`\begin{gathered} s\imaginaryI n^2\beta+cos^2\beta=1 \\ cos\beta=-(12)/(13) \end{gathered}`

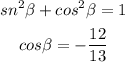
substitute

`s\imaginaryI n^2\beta+(-(12)/(13))^2=1`

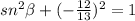
the angle beta lies on the III Quadrant -----> the value of the sine is negative

`\begin{gathered} s\imaginaryI n^2\beta=1-(144)/(169) \\ s\mathrm{i}n^2\beta=(25)/(169) \\ s\mathrm{i}n\beta=-(5)/(13) \end{gathered}`

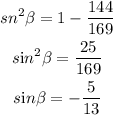
step 3

Substitute the given values in the formula of step 1

`\begin{gathered} cos(\alpha-\beta)=cos\alpha cos\beta+s\imaginaryI n\alpha s\imaginaryI n\beta \\ cos(\alpha-\beta)=(-(4)/(5))(-(12)/(13))+((3)/(5))(-(5)/(13)) \end{gathered}`
`\begin{gathered} cos(\alpha-\beta)=(48)/(65)-(15)/(65) \\ \\ cos(\alpha-\beta)=(33)/(65) \end{gathered}`