Question

Use the info given to solve the triangle round to nearest 10th

Answer 1

Triangle:

Procedure:

The interior angles of a triangle add up to 180°. As we know two angles, we can get the third as follows:

`m\angle L+m\angle K+m\angle J=180`

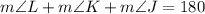
Isolating for m∠J

`m\angle J=180-m\angle L-m\angle K`

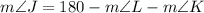
Replacing the values given:

`m\angle J=180-41-117`
`m\angle J=22`

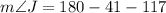
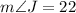
Then using the trigonometric functions, we can get the sides.

`(\sin (41))/(14)=(\sin (117))/(JL)`
`JL=(\sin(117))/((\sin(41))/(14))`
`JL\approx19.01`
`(\sin(41))/(14)=(\sin (22))/(KL)`
`KL=(\sin (22))/((\sin(41))/(14))`
`KL\approx7.99`

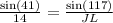
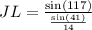
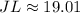
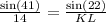
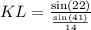
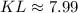
Answer:

• m∠J, = 22°

,

• JL = 19.01

,

• KL = 7.99