Question

The ratio of the length to the width of a rectangle is 5 to 2. Express the width of the rectangle as a fraction of the perimeter of the rectangle. I am not sure how to help my son do the problem.

Answer 1

The perimeter of a triangle is given by the following expression:

`P=2\cdot(w+l)_{}`

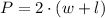
Where P is the perimeter, w is the width and l is the length.

We know that the ratio of the length to the width is 5 to 2. This means that for every 5 units of the length there are 2 units of the width, therefore:

`5\cdot l=2\cdot w`

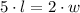
If we isolate the "l" variable on the left, we have:

`l=(2\cdot w)/(5)`

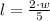
We can replace the expression above on the formula for the perimeter.

`P=2\cdot((2\cdot w)/(5)+w)_{}`

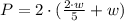
We now need to simplify the right side of the equation and isolate the "w" variable.

`\begin{gathered} P=(4w)/(5)+2w \\ P=(4w+10w)/(5) \\ P=(14w)/(5) \\ w=(5P)/(14) \end{gathered}`

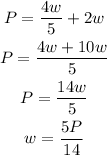
The width is equal to 5/14 of the perimeter.