Question

D Watch help videoIf PQ = 9, QO = 14, and TR = 35, find the length of ST. Round youranswer to the nearest tenth if necessary. Figures are not necessarily drawn toscale.818158R5841Submit AnswerAnswer: ST

Answer 1

Those triangles have 3 corresponding angles congruent to each other.

`\begin{gathered} \angle P\cong\angle S \\ \angle Q\cong\angle T \\ \angle O\cong\angle R \end{gathered}`

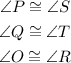
The AA Similarity Theorem states: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

By AA similarity, ΔPQO and ΔSTR are similar to each other.

If two polygons are similar, then the ratio of the lengths of any two corresponding sides is the same. QO corresponds to TR and PQ corresponds to ST, therefore, we have the following equation

`(TR)/(QO)=(ST)/(PQ)`

We have the measure of most of those sides. If we substitute those measures on this equation, we're going to have

`(35)/(14)=(ST)/(9)`

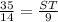
Solving for ST, we have

`\begin{gathered} (35)/(14)=(ST)/(9) \\ (5)/(2)=(ST)/(9) \\ ST=9\cdot(5)/(2) \\ ST=(45)/(2) \\ ST=22.5 \end{gathered}`

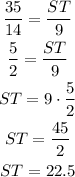
And this is our answer. ST = 22.5.