Answer:
56/8671
Explanation:
First, determine the total number of artworks.
• Sculptures = 10
,
• Sketches = 11
,
• Oil paintings = 9
Total = 10+11+9 = 30
20 artworks can be selected out of 30 in 30C20 ways.
Next:
• 4 sculptures can be selected out of 10 in 10C4 ways.
,
• 10 sketches can be selected out of 11 in 11C10 ways.
,
• 6 oil paintings can be selected out of 9 in 9C6 ways.
The combination formula is:

Therefore:
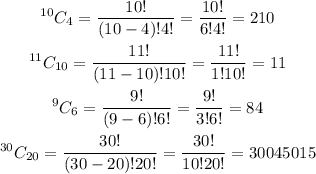
Thus, the probability that 4 sculptures, 10 sketches, and 6 oil paintings are chosen to be displayed is:
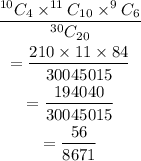
The probability is 56/8671.