Question

Determine whether each of the following trigonometric expressions is positive or negative

Answer 1

Given:

The trigonometric ratios are given as,

`\begin{gathered} \tan 143^(\circ) \\ \cos ((\pi)/(3)) \\ \sin 362^(\circ) \\ \csc ((3\pi)/(4)) \end{gathered}`

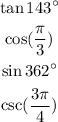
The objective is to find out which of these expressions is positive or negative.

Step-by-step explanation:

Consider the first expression and convert it as,

`\text{tan}143=\tan (90+53)\text{ . . . .(1)}`

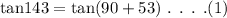
Using the trigonometric identities,

`\tan (90+\theta)=-\cot \theta`

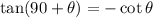
The equation (1) can be written as,

`\begin{gathered} \tan (90+53)=-\cot (53\degree)=-(1)/(\tan 53\degree) \\ =-0.754 \end{gathered}`

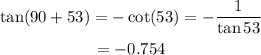
Thus, tan(143°) is a negative expression.

Consider the second trigonometric expression.

`\begin{gathered} \cos ((\pi)/(3))=\cos ((\pi)/(3)*(180)/(\pi)) \\ =\cos 60\degree \\ =(1)/(2) \end{gathered}`

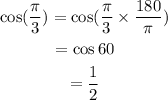
Thus, cos (π/3) is a positive expression.

Consider the third trigonometric expression.

`\begin{gathered} \sin 362\degree=\sin (360+2)=\sin 2\degree \\ \sin 2\degree=0.035 \end{gathered}`

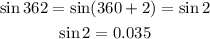
Thus, sin 362° is a positive expression.

Consider the fourth expression.