step 1
Solve the inequality 1
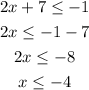
the solution of the inequality 1 is the interval
(-infinite, -4}
step 2
solve the inequality 2
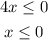
the solution of the inequality 2 is the interval (-infinite, 0}
step 3
Find the solution of the inequality 1 and the inequality 2
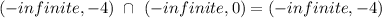
therefore
the solution set is (-infinite, -4}