When an exponent has another exponent on top of it, they can be multiplied.
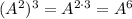
When two numbers with the same base are factors in a multiplication, their exponents can be added. The same for a quotient, but with the difference that the exponents are substracted (the number in the denominator is, in fact, the base with the negative exponent).
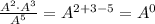
In the problem, we first appy the exponent power rule, in order to eliminate the parenthesis and have all the factors multypling:
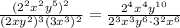
Then, to group the similar factors, we apply the product rule in the denominator, as the numerator is alrready simplified:
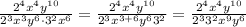
Now, we apply the quotient rule for the factors with the same base:
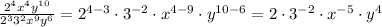
Finally, the negative exponents rule to put the numbers with negative exponents in the denominator with positive exponent:
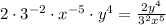
Order:
Expanded power rule
Product rule
Quotient rule
Negative exponent rule