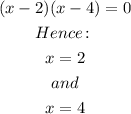*Take the constant term of the divisor with the opposite sign and write it to the left.
*Write the coefficients of the dividend to the right.
Therefore, the solution is given by:
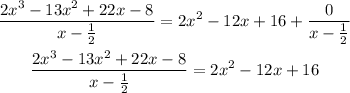
Therefore, the other solutions can be found as follows:
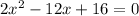
Divide both sides by 2:
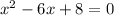
The factors of 8 that sum to -6 are -2 and -4, So: