ANSWER
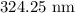
Step-by-step explanation
To find the thickness of the bubble at that point, apply the condition for constructive interference:
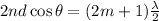
where d = thickness
n = refractive index
m = 0, 1, 2...
For the second longest wavelength, m = 1, and for normal incidence:
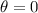
Therefore, substituting the given values into the equation and solving for d:
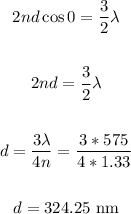
That is the thickness of the bubble.