Question

Each row of the table has two of the interior angle measures of two triangles.Which triangles are similar?Choose Similar or Not Similar for each pair of triangles.TrianglesSimilarNot SimilarTriangle 1: 15°, 45°Triangle 2: 45°, 120°Similar – Triangle 1: 15°, 45° Triangle 2: 45°, 120°Not Similar – Triangle 1: 15°, 45° Triangle 2: 45°, 120°Triangle 1: 90°, 45°Triangle 2: 45°, 45°Similar – Triangle 1: 90°, 45° Triangle 2: 45°, 45°Not Similar – Triangle 1: 90°, 45° Triangle 2: 45°, 45°Triangle 1: 130°, 35°Triangle 2: 25°, 130°Similar – Triangle 1: 130°, 35° Triangle 2: 25°, 130°Not Similar – Triangle 1: 130°, 35° Triangle 2: 25°, 130°

Answer 1

1. We have

`\begin{gathered} Triangle1\colon15\degree,45\degree \\ Triangle2\colon45\degree,120\degree \\ For\text{ Trinagle 1, 15 + 45 + 120 = }180,\text{ assume the 3rd angle is 120}\degree \\ \text{For Triangle 2, 45 + 120 + 15 = 180, assume the 3rd angle is }15\degree \end{gathered}`

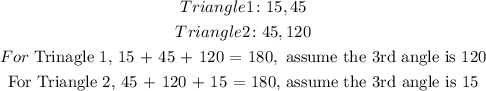
Since we got 180 in both, hence the two trinagles are similar

2.

`\begin{gathered} Triangle1\colon90\degree,45\degree \\ Triangle2\colon45\degree,45\degree \\ For\text{ Trinagle 1, 90 + 45 + 45 = }180,\text{ assume the 3rd angle is 45}\degree \\ \text{For Triangle 2, 45 + 45 + 90 = 180, assume the 3rd angle is 90}\degree \end{gathered}`

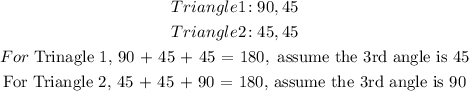
Since we got 180 in both, hence the two trinagles are similar

3.

`\begin{gathered} Triangle1\colon130\degree,35\degree \\ Triangle2\colon25\degree,130\degree \\ For\text{ Trinagle 1, 130 + 35 + 25 = }190,\text{ assume the 3rd angle is 25}\degree \\ \text{For Triangle 2, 25 + 130 + 35 = 190, assume the 3rd angle is 35}\degree \end{gathered}`

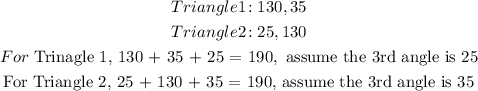
Since we got 190, the two triangles are not similiar because the sum of interior angles in any triangle must be equal to 180 degrees

Hence the triangles in number 3 are NOT similar