In the equation:
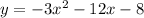
the leading coefficient, a, is equal to -3. Given that a is less than zero, then the parabola has the shape of a ∩. Therefore, it has a maximum.
To find the maximum, we need to find the vertex (h, k) of the parabola.
The x-coordinate, h, is found as follows:
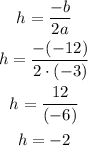
The y-coordinate, k, is found substituting the value of h into the equation of the parabola, as follows:
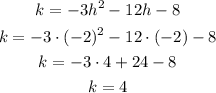
Then, the maximum is placed at (-2, 4)