Question

An architect has designed two tunnels. Tunnel A is modeled by x2 + y2 + 28x + 52 = 0, and tunnel B is modeled by x2 – 36x + 16y + 68 = 0, where all measurements are in feet. The architect wants to verify whether a truck that is 8 feet wide and 13.5 feet high can pass through the tunnels.Part B: Write the equation for Tunnel B in standard form and determine the conic section. Show your work. (4 points)I only need help with Part B

Answer 1

Tunnel A: Circle

Tunnel B: Parabola

Max height of A: 12 ft

Max height of B: 16 ft

The truck can only pass through tunnel B.

Step-by-step explanation:

Since we do not know what x and y represent, we assume that is the height of the tunnel and x is the width.

Part A:

Let us convert our equation into the standard form.

The equation for tunnel A is

`x^2+y^2+28x+52=0`

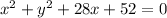
which we rewrite as

`(x^2+28x+\cdots)+y^2=-52`

Now we complete the square for variable x. What should we add to x^2 + 28x to make it a complete square?

After some thinking, we realise that we do x^2 + 28x + 14^2 then we have (x + 14)^2 .

Therefore, we add 14^2 to both sides of our equation to get:

`(x^2+28x+14^2)+y^2=-52+14^2`
`(x+14)^2+y^2=-52+14^2`
`(x+14)^2+y^2=144`

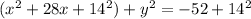
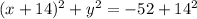
this equation we recognise as that of a circle! Therefore, the conic section for tunnel A is a circle.

Part B:

Let us now turn to tunnel B and write its equation:

`x^2-36x+16y+68=0`

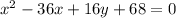
The first thing to note is that the above equation is linear in y; therefore, we can rearrange the equation to write it as

`16y=-(x^2-36x+68)`

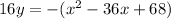
Now we have to complete the square on the right-hand side.

subtracting 256 from both sides gives

`16y-256=-(x^2-36x+68)-256`
`16y-256=-x^2+36x-324`
`16y-256=-(x^2-36x+324)`

`16y-256=-(x-18)^2`
`\Rightarrow y=-(1)/(16)(x-18)^2+(256)/(16)`

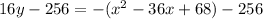
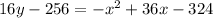
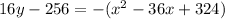
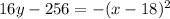
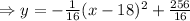
which is the standard equation for a parabola!

Hence, the conic section for tunnel B is that of a parabola.