Answer:
18037.5 J
Step-by-step explanation:
The work done by friction is equal to the change in the kinetic energy, so it can be calculated as
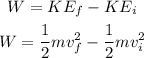
Where m is the mass, vf is the final velocity and vi is the initial velocity.
Replacing m = 325 kg, vf = 17 m/s and vi = 20 m/s, we get
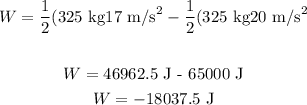
Therefore, the work done by friction is 18037.5 J against the movements.