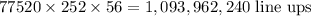Question

15 cars are going to be lined up at a dealership.The first 7 must be convertibles, then next 5must be SUV's, and the last 3 must be vans. Ifthere are 20 convertibles, 10 SUV's, and 8 vansto choose from, how many distinct line ups canbe created?

Answer 1

- This is a combination question because we are to choose from a list of items in a distinct lineup.

- The formula for combination is:

`\begin{gathered} ^nC_r=(n!)/((n-r)!r!) \\ \\ where, \\ n\text{ is the total amount of items} \end{gathered}`

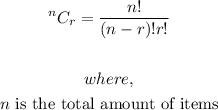
- Also, since the choice or distinct arrangement of the cars independent, we can simply multiply the possible combinations.

- That is,

`\begin{gathered} \text{ Convertible:} \\ ^(20)C_7=77520 \\ \\ \text{ SUV:} \\ ^(10)C_5=252 \\ \\ \text{ Vans:} \\ ^8C_3=56 \end{gathered}`

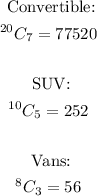
- Thus, the possible number of distinct line ups is:

`77520*252*56=1,093,962,240\text{ line ups}`