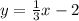Question

Write the equation of the line that passes through the points (-3, -3) and (12,2).

Answer 1

We are to find the equation of the line joining the points

`(-3,-3),(12,2)`

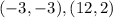
The equation of a line is given as

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`

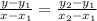
From the given points we have

`\begin{gathered} x_1=-3,x_2=12 \\ y_1=-3,y_2=2_{} \end{gathered}`

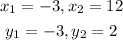
Therefore, the equation of the line is

`(y-(-3))/(x-(-3))=(2-(-3))/(12-(-2))`

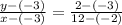
This gives

`(y+3)/(x+3)=(2+3)/(12+3)`

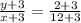
Simplifying this we have

`\begin{gathered} (y+3)/(x+3)=(5)/(15) \\ (y+3)/(x+3)=(1)/(3) \end{gathered}`

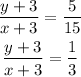
This further gives

`\begin{gathered} 3(y+3)=x+3 \\ 3y+9=x+3 \\ 3y=x+3-9 \\ 3y=x-6 \end{gathered}`

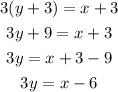
Dividing both sides by 3 we get

`\begin{gathered} y=(1)/(3)x-(6)/(3) \\ y=(1)/(3)x-2 \end{gathered}`

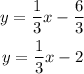
Therefore, the equation is

`y=(1)/(3)x-2`