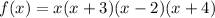Question

Select a function f whose zeros are 0, negative 3, 2, and negative 4.

Answer 1

All the alternatives are polynomials. In a polynomial in factored form, each factor corresponds to a zero of the function.

If r is a zeros of the polynomial function, it will have a factor:

`(x-r)`

So, if 0, -3, 2 and -4 are zeros of the polynomial, we have the factors:

`\begin{gathered} (x-0)=x \\ (x-(-3))=(x+3) \\ (x-2) \\ (x-(-4))=(x+4) \end{gathered}`

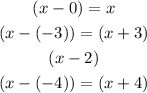
So, the function that has these zeros is:

`f(x)=x(x+3)(x-2)(x+4)`