Answer:
Centre: (2, 1)
Radius: 7
Step-by-step explanation:
If we have an equation of the form
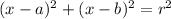
then the centre of the circle is located at (a, b) and the radius is r.
Now, in our case we have
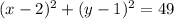
which can be rewritten as
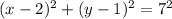
which tells us that the centre is at (2, 1) and the radius is 7.
The graph is attached below.