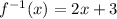Question

F(x) = (x - 3)/2 which of the following equations represents f ^ - 1 * (x) ?

Answer 1

We are given the following function:

`f(x)=(x-3)/(2)`

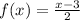
We are asked to determine:

`f^(-1)(x)`

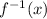
This is called the inverse function.

To do that we will first switch the value of the variables f(x) and "x" as follows:

`x=(f(x)-3)/(2)`

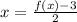
Now, we will solve for f(x). To do that we will multiply both sides by 2:

`2x=f(x)-3`

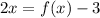
Now we add 3:

`2x+3=f(x)`

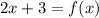
This is the inverse, therefore, we change:

`f(x)=f^(-1)(x)`

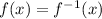
Therefore, we have:

`f^(-1)(x)=2x+3`