In order to calculate the length of the mid-segment of a trapezoid we can use the following formula:
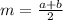
Where m is the length of the midsegment, a and b are the lengths of the top and bottom bases.
By replacing x for m, 22 for a and 4 for b, we get:
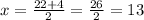
Then, x equals 13
The midsegment splits the side BC into two equal-length segments, BM and MC, then the lengths of these segments is the same and we can formulate the following expression:
BM = MC
BM = 8
As mentioned, segment BC is formed by segments BM and MC, then by summing up the lengths of these two segments we get the length of BC, like this:
BC = BM + MC
BC = 8 + 8
BC = 16
Then, BC equals 16
For isosceles triangles, angles in opposite bases are supplementary, then we can formulate the following expression:
mmm
Then, ADC equals 115°