Question

Solve the system by elimination.5x - 3y + 4z = 3- 4x + 2y - 3z = -1-x + 5y + 7z = -6Pls see the picture

Answer 1

Adding 5 times the third equation to the first one we get:

`\begin{gathered} 0x+22y+39z=-27, \\ -4x+2y-3z=-1, \\ -x+5y+7z=-6. \end{gathered}`

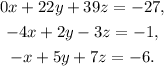
Multiplying the third equation by -1 we get:

`\begin{gathered} 0x+22y+39z=-27, \\ -4x+2y-3z=-1, \\ x-5y-7z=6. \end{gathered}`

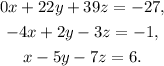
Adding 4 times the third equation to the second one we get:

`\begin{gathered} 0x+22y+39z=-27, \\ 0x-18y-31z=23, \\ x-5y-7z=6. \end{gathered}`

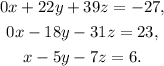
Dividing the first equation by 22 we get:

`\begin{gathered} 0x+y+(39)/(22)z=-(27)/(22), \\ 0x-18y-31z=23, \\ x-5y-7z=6. \end{gathered}`

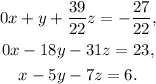
Adding 18 times the first equation to the second one we get:

`\begin{gathered} 0x+y+(39)/(22)z=-(27)/(22), \\ 0x+0y+(10)/(11)z=(10)/(11), \\ x-5y-7z=6. \end{gathered}`

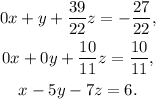
Adding 5 times the first equation to the third one we get:

`\begin{gathered} 0x+y+(39)/(22)z=-(27)/(22), \\ 0x+0y+(10)/(11)z=(10)/(11), \\ x+0y+(41)/(22)z=-(3)/(22). \end{gathered}`

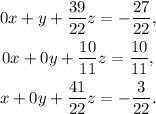
Multiplying the second equation by 11/10 we get:

`\begin{gathered} 0x+y+(39)/(22)z=-(27)/(22), \\ 0x+0y+z=1, \\ x+0y+(41)/(22)z=-(3)/(22). \end{gathered}`

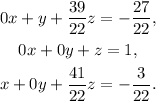
Subtracting 39/22 times the second equation from the first one we get:

`\begin{gathered} 0x+y+0z=-3, \\ 0x+0y+z=1, \\ x+0y+(41)/(22)z=-(3)/(22). \end{gathered}`

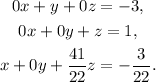
Subtracting 41/22 times the second equation from the third one we get:

`\begin{gathered} 0x+y+0z=-3, \\ 0x+0y+z=1, \\ x+0y+0z=-2. \end{gathered}`

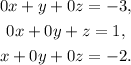
Therefore, the solution to the given system of equations is x=-2, y=-3, and z=1.