Given:
At the city museum, child admission is $5.80 and adult admission is $9.00.
Let the number of children's tickets = x
And the number of the adult tickets = y
on Monday 162 tickets were sold ⇒ x + y = 162
The tickets were sold for a total sale of $1176.40 ⇒ 5.8x + 9y = 1176.40
So, we have the following system of equations:
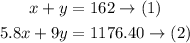
From equation (1) x = 162 - y
substitute (x) into equation (2)
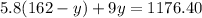
Solve the equation to find (y):
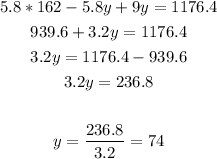
substitute (y) to find (x)
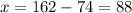
So, the answer will be:
The number of children tickets = 88
The number of adult tickets = 74