ANSWER
The number of ways of obtaining a committee with exactly 3 Republicans is 7280 ways
Explanation:
Given information
A committee of 8 representatives will be selected from a group of 14 Republicans and six Democrats.
From the above information
The total number of persons = 14 + 6
The total number of persons = 20
The total number of ways of selecting 8 representatives is 20C8

The favorable way of selecting exactly 3 republicans are 14C3(6C3)
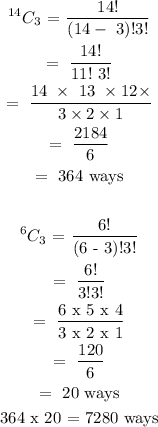
Therefore, the number of ways of obtaining a committee with exactly 3 Republicans is 7280 ways