Question

Find a degree 3 polynomial that has zeros -1, 4, and 8 and in which the coefficient of x^2 is -22. The polynomial is: ______

Answer 1

2x^3 - 22x^2 + 40 x + 64

Step-by-step explanation:

First, we take care of the roots.

The roots of the polynomial are - 1, 4, and 8 which means that it should look like

`\begin{gathered} (x-(-1))(x-4)(x-8)_{} \\ \Rightarrow(x+1)(x-4)(x-8)_{} \end{gathered}`

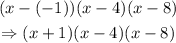
Note that the above polynomial would be of degree 3 since we are multiplying three terms containing x.

Expanding the above polynomial gives

`\begin{gathered} (x+1)(x-4)(x-8)=x^3-11x^2+20x+32 \\ \end{gathered}`

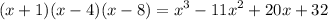
Now we note that the coefficient of x^2 is -11 in the above polynomial; however, we want it to be -22. So what do we do? If we multiply the polynomial by 2 we get

`2(x^3-11x^2+20x+32)=2x^3-22x^2+40x+64`

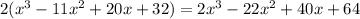
The coefficient of x^2 is now -22 and so our condition is satisfied!

Hence a 3 degree with roots -1, 4 and 8 and with x^2 with a coefficient of -22 is

`2x^3-22x^2+40x+64`

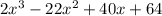
which is our asnwer!