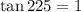We are asked to determine the value of sine, cosine, and tangent of the given angle using the reference angle. The reference angle for quadrant III is the angle minus 180, that is:

using these angle we have the following:
To determine the value of "x" we use the function cosine, since this is defined as:
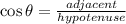
Replacing the values:
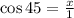
Since:
![\cos 45=\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/kgdbc0lyms82xzg3w38962u0272mwkgsns.png)
Replacing:
![x=\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/zhp3j9cjsc9a41rmgvzp0j25rppe2zjlvl.png)
We find "y" using the sine function:
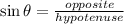
Replacing:
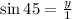
we have:
![\sin 45=\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/hqekvp07g1l6ubdsvo7rtqttttyvwsnf2l.png)
therefore:
![\frac{\sqrt[]{2}}{2}=y](https://img.qammunity.org/2023/formulas/mathematics/college/tam3vdtlz0cb28m070nexsnjb1mykr7dli.png)
Now, since we have a reference angle, the values for quadrant III are:
Therefore, the values of the functions for 225 degrees are:
![\sin 225=-\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/len0lci79q6dgfpytoez7unovmbekr15cs.png)
![\cos 225=-\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/1dc03plfwp6dnia3kjpy462sp3lyz1vmsu.png)
The tangent function is defined as:

Replacing the known values:
![\tan 225=\frac{-\frac{\sqrt[]{2}}{2}}{-\frac{\sqrt[]{2}}{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/9yzy71nw25ng1ahrjo5g4xg61agi4ukg3c.png)
Solving: