Solution:
Given:
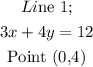
To get the equation of the second line, it has the same slope as Line 1 because the two lines are parallel.
Hence, the slope
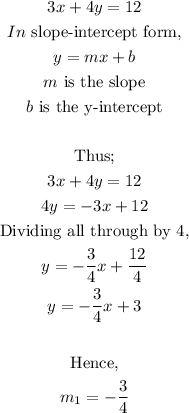
To get the equation of the second line parallel to line 1, then;

The equation of the second line is gotten by the formula;

Thus;

Therefore, in slope-intercept form, the equation of the line parallel to 3x + 4y = 12 through the point (0,4) is;
