Question

Hello! I need some assistance with this homework question for precalculus, please?HW Q11

Answer 1

Given:

`5^(2x+1)=125`

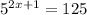
We will solve the exponential equation to find (x)

First, we will make a prime factorization of 125

125 = 5 * 5 * 5 = 5³

So, the given equation can be written as follows:

`5^(2x+1)=5^3`

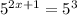
both sides have a base of (5), so the exponents are equal

we can write the following equation:

`2x+1=3`

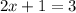
Solve the equation to find (x)

`\begin{gathered} 2x=3-1 \\ 2x=2 \\ x=(2)/(2)=1 \end{gathered}`

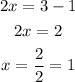
So, the answer will be x = 1