Question

Your initial speed is zero. If you increased your speed by 4 m/s after only 2seconds and continue to accelerate at the same rate, what will your speed beafter 10 seconds?A. 40 m/sB. 20 m/sC. 30 m/sD. 10 m/s

Answer 1

Given:

Initial speed, u = 0 m/s

Final speed = 4 m/s

Time, t = 2 seconds

Given that acceleration remains the same, let's find the speed after 10 seconds.

Apply the formula:

`v=u+at`

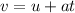
Where:

v is the final speed

u is the initial speed

a is the acceleration

t is the time.

Hence, we have the equation:

`4=0+2a`

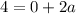
Let's find the acceleration (a) from the equation above.

Divide both sides by 2:

`\begin{gathered} 4=2a \\ \\ (4)/(2)=(2a)/(2) \\ \\ 2=a \\ \\ a=2 \end{gathered}`

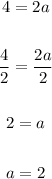
The acceleration is 2 m/s^2.

After 10 seconds, given that the acceleration is the same, we have:

`\begin{gathered} v=u+at \\ \\ v=0+2(10) \end{gathered}`

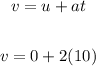
Let's solve for the speed v.

`\begin{gathered} v=0+20 \\ \\ v=20\text{ m/s} \end{gathered}`

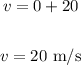
Therefore, the speed after 10 seconds will be 20 meters per second.

ANSWER:

B. 20 m/s