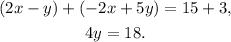We have a system of two equations:
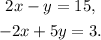
We want to reduce the system to an equation with only variables, we see that by adding the equations we can achieve that. This is because the terms with x cancel each other:
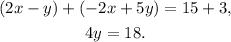
Answer
i) Variable x is ready to be eliminated.
ii) Adition is required to eliminate the variable.
Reason: by adding the equations we see that variable x is eliminated: