EXPLANATION
Given the triangle, we can calculate the value of the other angles by applying the Law of Sines as we already know,
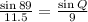
Multiplying both sides by 9:
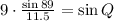
Switching sides:
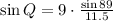
Simplifying:
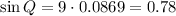
Applying sin-1 to both sides:
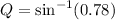
Computing the argument:
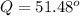
Applying the Triangles Sum of Interior Angles Theorem give us the following relationship:
89 + 51.48 + P = 180
Adding like terms:
140.48 + P = 180
Subtracting 140.48 to both sides:
P = 180 - 140.48 = 39.52 degrees
The answers are:
Q=51.5°
P = 39.5° ---> Rounding to the nearest tenth