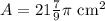Step-by-step explanation
The area of a section of a circle with radius 'r' and central angle 'a' in radians, is:
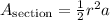
In this problem, the radius is 7cm and the central angle a is 160º. Since you're asked to express the result in terms of pi we have to convert this angle from degrees to radians:
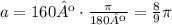
Now we can find the area:
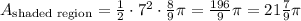
Answer
The area is:
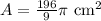
Or expressed as a mixed number