Given:
a.) Suppose that Juan found a crop circle with a 1350 ft radius.
b.) He follows a 2000 ft arc on the circle.
To find the central angle, we will be using the following formula:
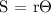
Where,
S = Arc Length = 2000 ft.
r = radius = 1350 ft.
Θ = Central angle (in radians)
We get,
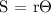
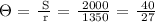
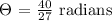
Therefore, the answer is 40/27 radians.