We have to check which one of the numbers given are solutions of the equation:
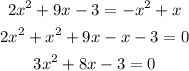
For doing so, we will replace each one of the values onto the equation, and if both sides of the equation remains the same, we will get a solution.
a: x=-2
In this case,

And as it's not equal to zero, its not a solution.
b: x=1/3
In this case
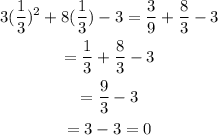
And as it's equal to zero, it's a solution.
c: x=1
In this case

So, 1 is not a solution
d: x=3
In this case,
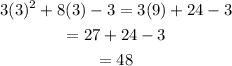
So 3 is not a solution.
e: x=-1/2
In this case,
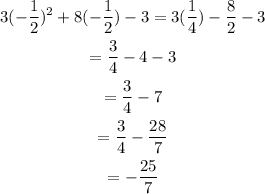
So -1/2 is not a solution.
f: x=-3
In this case,
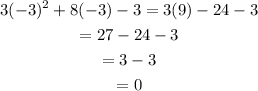
This means that 3 is a solution of the equation.