Given the exponential function:
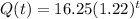
Let's find the initial value P, growth /decay factor a, and growth/decay rate r.
Aply the general exponential formula:
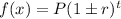
Here, we have:
P = 16.25
Growth factor, a = 1.22
If the factor is less than 1 it is an exponential decay function.
If the factor is greater than 1, it is an exponential growth function.
To find the value of r, we have:
1 + r = 1.22
r = 1.22 - 1.0
r = 0.22
Therefore, the growth rate is 0.22 or 22%.
ANSWER:
(c). The growth rate is r = 0.22