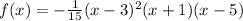Solution
The graph of the polynomial f(x) is given below. If f(x) has degree 4, find the factored equation for f(x).
Given graph solution as degree is 4
The four roots are x = -1 , x = 3, x = 3, x = 5 where the graph passes through x-axis
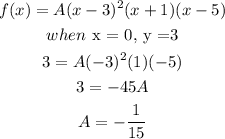
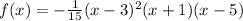
Since the f(x) has degree 4
Hence the answer is :