Proportions
We are told that y varies directly as x and inversely as the square of z. This can be written as:
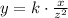
Where k is the constant of proportionality. The value of k can be found by using the given point: y = 39 , x = 52 , z = 2
Substituting:
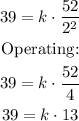
Solving for k:
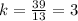
The relationship is now:
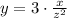
Now we use the equation to know the value of y when x=18 and z=3:
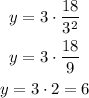
y = 2