Question

Donna correctly states that the measure of an interior angleof a square is 90°, and the angle of rotational symmetry of the square is 90°. Then shestates that the angle of rotational symmetry of an equilateral triangle is 60° because themeasure of an interior angle is 60°. Explain her error.

Answer 1

Given data:

The angle of rotational symmetry for square is,

`\begin{gathered} A=(360^(\circ))/(4) \\ =90^(\circ) \end{gathered}`

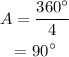
The angle of rotational symmery for equilateral triangle is,

`\begin{gathered} B=(360^(\circ))/(3) \\ =120^(\circ) \end{gathered}`

Angle of rotational symmetry of the regular polygon is sum of the central angle divided by number of sides of polygon.

Thus, the measure of the interior angle concept is wrong.